Write-up for mathjail2

This is a write-up for a crypto/golf challenge from jailCTF 2025 called mathjail2.

I played jailCTF 2025 last weekend with hashkitten fan club. It was a close fight against chr(sum(range(ord(min(str(not())))))) but we ended up winning, so big thanks to everyone else who carried.

Screenshot of final scoreboard

I wasn’t originally planning to commit much time to this CTF, but Lyndon believed in me so much I had no choice but to solve mathjail2.

Challenge details

Code for chal.py

#!/usr/local/bin/python3
from typing import Callable, Iterator, Tuple
from hashlib import sha256
import random


class MathJailError(Exception):
    pass


class MathJail:
    title: str
    description: str

    def __init__(self, max_size: int):
        self.max_size = max_size

    def run(self, code: str) -> bool:
        func = self.validate(code)
        for input, output in self.gen_test_cases():
            user_output = func(input)
            if not isinstance(user_output, int) or user_output != output:
                return False
        return True

    def gen_test_cases(self) -> Iterator[Tuple[int, int]]:
        raise NotImplementedError

    def validate(self, code: str) -> Callable[[int], int]:
        if len(code) > self.max_size:
            raise MathJailError(f'Code is too large ({len(code)} > {self.max_size})')

        for c in code:
            if c not in '0123456789n+-*/%^&|<~>()':
                raise MathJailError(f'Illegal character: {c!r}')

        try:
            func = eval(f'lambda n: {code}', {}, {})
        except Exception as e:
            raise MathJailError(f'Could not compile expression: {e}')
        return func

    def __repr__(self):
        return self.description


class SHA256Jail(MathJail):
    title = 'SHA-256'
    description = 'Write an expression that takes a 64-byte string\n' \
                  'and outputs its SHA-256 hash (in big-endian).\n'

    def gen_test_cases(self):
        random.seed(0x1337)
        for _ in range(256):
            s = random.randbytes(64)
            n = int.from_bytes(s, 'big')
            output = int.from_bytes(sha256(s).digest(), 'big')
            yield (n, output)


if __name__ == '__main__':
    print('You thought you escaped, but the Warden has one last trick. The exit is sealed by a lock\n'
          'that only answers to SHA-256. One level, one shot - hash your way to freedom.\n')

    jail = SHA256Jail(19850)
    print(f'Level X: {jail.title}')
    print('-' * 30)
    print(jail)

    code = input(f'Enter your expression ({jail.max_size} characters max): ')

    try:
        result = jail.run(code)
    except Exception as e:
        print(e)
        exit(1)

    if not result:
        print('You have failed.')
        exit(1)

    with open('flag.txt', 'r') as f:
        print(f"Your victory is well-deserved: {f.read()}")

There’s a lot of boilerplate in the code, so let’s try to reduce it to the bare minimum of what is required.

Basically, you have to construct a function f, such that f(n) gives you the SHA256 hash of a 512-bit n (both input and output are treated as ints). There are 256 test cases, which is known beforehand.

The function itself is defined as f = lambda n: {code} where code can only consist of characters in “0123456789n+-*/%^&|<~>()”. Basically it’s going to be a pure mathematical function.

But most importantly, there is a significant golfing component – len(code) must be at most 19850.

Solving the challenge

Attempt 1

Let’s for now assume we have square brackets and commas. A natural thing to try then would be to have:

1. a length-256 array consisting of all the output values, and
2. a “perfect hash” from our input set into {0,1,2,…,255}, so we can just index from the above array

It turns out we don’t even have enough characters for the first! A 256-bit value can have up to len(str(2^256))=78 characters. And 256 of these would have 19968 characters already, exceeding our golf limit! And this isn’t counting the commas.

Well, actually we could just concatenate (bitwise) all the values, so we get a single large 65536-bit number instead. This only thas length len(str(2^65536))=19729 which is below the limit. And then we can index it by taking the relevant 256 bits: (BIGNUM >> (256 * h(n))) % 2**256, where h(n) is the perfect hash.

Ok, well that gives us no more than 120 chars with which to build our perfect hash. Unfortunately we couldn’t find a concise way to do this. Here’s a 417-char perfect hash:

n*1073%3852*21%1618*79%1332*95%1162*27%982*127%891*41%792*190%733*284%677*563%630*113%603*129%574*284%541*3%517*59%494*250%477*179%462*125%432*107%419*5%408*193%390*261%382*44%373*247%363*17%351*143%345*46%337*273%332*22%327*281%321*187%316*245%309*297%304*139%299*98%295*99%290*22%287*82%285*247%283*37%280*125%278*145%276*106%273*190%271*24%269*21%268*17%267*177%266*19%264*167%262*14%261*57%260*191%258*254%257%256

It consists only of * and %. Actually I later got it down to just under 400 chars but I can’t seem to find where I recorded this down. Regardless, this is way more than the required 120 chars.

So this attempt is a failure, and we need a different strategy.

Attempt 2

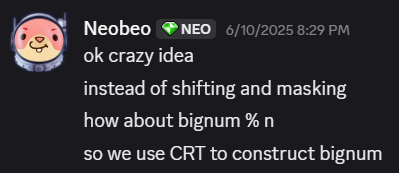
I brainstormed a bunch of crazy ideas, but this one turned out to be key. Instead of a perfect hash, we just needed a map from n to some set of values that could be used for CRT. This means the numbers had to be:

1. pairwise coprime (can be elided if the outputs had the same value modulo the common prime, but for simplicity let’s just make all the moduli pairwise coprime)
2. each modulus has to be larger than the output value, so 256-bits
3. each modulus cannot be too large, otherwise bignum will be too big

So we will aim for each modulus to be approximately 2^256. This is easy enough to aim for, we could just take 2**256 + n%(some small number) to get the right order of magnitude.

Then making it pairwise coprime will be the difficult bit.

Let’s look at how likely our numbers are to be pairwise coprime if they’re picked randomly.

For each prime $p$, we want exactly 0 or 1 of our 256 numbers to be divisible by $p$. This happens with probability $\left(\frac{p-1}{p}\right)^{256}+256\frac{1}{p}\left(\frac{p-1}{p}\right)^{255}$. Or in tabular form:

 p   above probability
---  --------------------
 2   2.21949531865927e-75
 3   1.07455188919647e-43
 5   1.00913675999546e-23
 7   3.17520591912740e-16
11   6.73525799557265e-10
13   2.81743785598410e-8
17   3.09200799681282e-6
19   0.000014836023761924
23   0.000144378453330621
29   0.00127270828182582
31   0.00215621650001986
37   0.00729254614619101
41   0.0133021603724717
43   0.0171735740547756
47   0.0266810176547394
53   0.0451627860783698
59   0.0680695729916457
61   0.0765276130676887
67   0.103850823207220
71   0.123333351017914
73   0.133354674245348
79   0.164185493444228
83   0.185121734115143
89   0.216669678928182
97   0.258311128297240

And we’d need to multiply over these probabilities for all primes $p$, not just the ones under 100 as listed above. The overall probability is success is extremely small, something like $10^{-224}$. So we need to refine this a bit.

What if we ensured that none of our 256 moduli had a prime factor under 100? We can ensure this by rounding each modulus to the nearest multiple of 100 primorial (i.e. product of all primes under 100), then adding 1.

Or in pseudo-code, let q = 2 * 3 * 5 * ... * 97. Then we could have something like

mod = (2**256 + n%(some small number)) // q * q + 1

Doing this improves our probability from $10^{-224}$ to $10^{-15}$. Not terrible at all. What if we keep taking more primes? We can only take at most the first 43 primes, because if multiply the 44th prime the primorial already exceeds $2^{256}$ which means our modulus will be too big. Using 43 primes we have a probability of $10^{-9}$, which is quite a bit to brute force. Though probably doable.

Attempt 2.1

If 256 moduli is too big, why don’t we just break it down into smaller problems? One formula for when n%2==0 and another formula for when n%2==1. Turns out we have 134 instances of the former and 122 of the latter.

With only 134 moduli instead of 256, our probability of succeeding converges really quickly! Using 43 primes gives $10^{-3}$, using primes under 100 gives $10^{-5}$, and using the first 17 primes gives $10^{-8}$. We arbitrarily decide that $10^{-8}$ is a good enough cutoff so we use 17 primes.

This means we settle with q = 1922760350154212639070 (product of first 17 primes).

Now, since we’re golfing, it’s a waste of add 2^256, then divide by q, then multiply by q. So instead we note that 63^31 * q is just about 2^256, and is in fact larger than all of our output values. In that case, the moduli we want must have the form:

mod = (n%(some small number) + 63**31) * q + 1

where we can just brute force some small number and there’s a $10^{-8}$ probability of success.

For n%2==0 (with 134 items), it turns out 9889608 is the smallest way to do this. So we have

mod = (n%9889608+63**31)*1922760350154212639070+1

and for n%2==1 (with 122 items), this is much more common, so we take one that’s “near” the other value:

mod = (n%9948988+63**31)*1922760350154212639070+1

There are smaller values, but why do we choose this one? It’s because the closeness to the other value allows us to golf this as

mod = (n%(9889608+n%2*59380)+63**31)*1922760350154212639070+1

and at this point we are more or less done. But again, we recall that we have have BIGNUM0 % mod for when n%2==0 and BIGNUM1 % mod for when n%2==1. Where BIGNUM0 and BIGNUM1 have length 10326 and 9402 digits respectively. We can reuse the same trick and write BIGNUM0+n%2*(BIGNUM1-BIGNUM0) and everything just works out!

That’s basically it then. Our final payload, of length 19793 chars, is:

(685622082900917457926873907876313263043456623136348799676292662988130695407466149203832701128962493129529426937527293318030430817785235943142148628190475945118119167522334766453401943545796781983597943710992425763851150317704520843574980722168674174812686877918201639977119225145387114281246060564109576392414192311290141238946372147927379763812845207301733505707544550128609772663891868852074309594155209587668538241224116837870007110898243060249765916426196436999056922059573964270204351675841386747601994135667274717644698707436771383125798466572459849242581537098985987734484671765203875793772151186469236352665913669781128294913697700076004601231390938090463169798021368557708749597332095357312973313808813990991309647827784741089430122675406320518711726686627471570580060853405032786773817950367882227705969720303209504691633055612160993639064276627754006694922906630980264005495409550380061396625402888168691244016721012377620193443915707828791071081592293454526719757260082911069513610287655802235868728101858548443470097236413611744347143443464861434531626593417225702349332381709735522621470752585508736394553388243337552924910446451795175691862361063338137400732015585006427126027607996151877095315262290054186390883995534027532027081011795664387335007950316057649605026934098091365552670131163020534553658404062510692506136519815371150273862125460295414925248557659343094960215787423721037291600179615359189415961032337867815331946437011913039519060576449155837657577872324727755652744288670425799809001645015828103608881753297049680891743881698842660226498738487451586312663374327868516920470105673972225785561728575802187855875574952956660057821448814388966589244524130929437123237956689839452964708245871832471715261253893733767636207319835184457643310452870879413561185984268819445224405038977453027389992336766077889979329648916973400067868965842453413293078583536298283194548267588553180456362522005688300719585337159757643714735756105894386161509764989190318074274745785679925508900243596844152427340191119306788857149709774567094980842227512506724559123131421275224945715905621899040210567257500796684366011945915830214825361571126889102016232442596490355153240958896080502198549603045759617784521941497570359515444854073148263734982860115999780003996762584385305101860628499304689581391014256652880251347872454987208861683385472849624894231838100066994411491779536205807094155471880851552492160491913679615144791783002703629887421274266393759910858168203431114882334453724206652523073671310609849800061250159493631690112211428903609246383419117866949842689409348016125790107839030359722833346798871479145345052239607067622768196845989197735507939332707710073935547310772281428443373792453499479972131046043582204628335781154569214467272276068176540755256916832135444379840113886704827767276974605285738757459925406372174035571914534141521463619908455709490013215334542101709645787748154177283108600551021531277609517247665218207350222529489014745359192488120209712598872315512032401728567657438610560667650860354780578087647593989086590240089253224029863016808636146152776921511532907598352953925584214428456391165629805035933471020060580529033025357797217868170106596236275106359572497289419386475139730539916547579902871308325159244049426137313730680508623613766615068684932665468393660357855402354380628360914841954431738313318003587257264769461705292613983437709496347042834236809992306393935108230768184897736527659822378115428608293854882142143159900683663187127037065352356219491775629542491431481694525020125359158703868274136570653668955984202524812850015929953391144003598272150428068877612239399052989436726916507991746137587533229535160159088472617138627969723523022629803529454919412604102439986615837339086883720154779895726216062932200733221224609328532047674394236559450133773638649750520824254310749278150896874033807953832798914810419095117481484429929821930753066297631523719004847569068357480427581737947503040182135235410959352362115074980344622804187012894955701718151638777047209839174637865171426692864857208886355625427905407355679952901742675574998592538931820548685482123910654266165071553375924500868515550332991081577769280300261163188327357684009951391503895815296592158869856050968105857136732878936199402172359287542971269342977347631685020995547607951883391145291159526098722514434667280183603303712600365965542692940156802885704326681386804023791879764623345622386876080176460385685423206365953480350399711194971620467735400339328725060687648081014399002653044240022658363589992600395916504298049398114840610745636315856387878936837290653764543921971852528264200417586263157748058588806077697282179541361343973750930647007461632832865269938727007656148666194891116795732367792512550640449943560191314573058956600775485653605336576470253661920655334271354954541177111201823721998921034200269490464821111043123085805376110142943771545421186911990335139988296253210890362347956657987345102872559287403051491800211283941507168225648695450972246600823927218618016272701694003088229123768880371576062409604771758309210131035744825643213320209945395056663111280168741654538735273297769182007481532990685662685930200048746268330217770786319852589620905907348540828230265956812705184328417729730477795486132375314632079887544474060003348722703441410169468941095742592072400278626286780755104827850431770110147493258756136829927914762087540573077125199481329420158969061602822133089841446849208922380400165425086668618895161948406117428108244822939162896708022717582534272007851180123882424233548019951690248378432803329083072028478875585199762601760994813312795067905064880237261765777420285114096385101987185558095382984420648043057099016343750458276946594634674391975339744536961720735483152130982294866487931390251444922848646411079727554168670860236120864790011285851307285058955412666476136138237352041936702873032983785349294094255577274605905176475670761675010041283563094157055742173222994867601422508811723896646852683092072696038957541610123384386848688476886013738892509794990674885727457779630635308889336324769495831133340542868941135441234192206707991447676203853699456393632922545812041283959731621128667753261575525629255397047668128278637881737381990432560943841632506236838861109350611454746578517297944161863407465087527141457529050403382895303527989751651914200828133913559250427871298600685130710334527904675631647246122305653760210787683766338274758745926828536349406283225952534489732110222201432500958723674031453858543606334459129310797010570779142499633967113170792204504664378820523870529597571431253982047785241016511739963783407614760695106936372920716886514817658110807447557641847658787736741039195586754447119735045342388085051801481989164251125083927847143156660184372689257657612796281632745568202616590575160147171190624479261682770363307888193580994518820792793948530188995158555530069367260938486577193570565721310084132311831997432379492445637068429191227302901949401581662665333575811227204744333696531205218732509887836983885739762963141884502306774509103121559369414903161136790343349558809618129921434736815608184496239813476068775015793104135811823555070639672895528014491081987178365394891160065146303185198355702474089831566331595427902687027990365804854781387674760063458187406518131278047222951083599075948919747237712411119385225347366912447107874353483116210029999104547747736026177752607603748730628435562432155131475647589521591839167495608150789870737899582802450107939071262264271890856172334687058831584001162605363732233633575530361386537045000772277420112812802870265849265400197292663761051977615414325314561355385818466012906694928613054806133288120468051203875209181748925785689591874480795231982481725384169853240989768797186778833598722345393319153478898298766286475668501700759995760960817574891026775160092840249635182745712924292106314630479605717675480202307020010944997604911415247240090955848295013458967666411849749537366729827351393772337726315885009249734527773115793033254693284233310682299033382903332327226224273404168917965047894466184857874709984759336357470062358250098686966472196049164730329728623459713631942088328653966591341422022580585921333498806892859346965074358495422267735275839581152936507270919669292819886761601964921247466260832887855859080458009870546527491652324069520271564107085031820455014431980544957753847540833662228688416124469268272917453967860280597232369729176657562016954489873581210699461178135573528133398439784629172998208853106024481836871660633853600931001493644934167934783272292506304271910171679618615245557814122166380667740449384134131201196394687871716278189273391213590431190402337716929620422541147180037029673244808943471026349023239414458531540280520611615726075571654333671554144060053257234298760305420702954334516903195490817777804119834606498139290046648990583636438657999009687879402359315763650767758950094784456198222209513986262239104860917646491840042763021818453813984158078346164409217406430878003313556089044444169900567981254259916405633196293953770340450890972552923308853932584934506706107035766797390805983338053651837557863393683040658625500472368873463746910708401808717072267432874955957928635180669952512540357034808062986479804737581556192818952969350825380170157204575734339251421888645515882382798460331134227034008235649138725210803127927679370770693458669205680981571050770681513472119983168350315488312888537621906605899037018403403149065233389620591960956094563761264835599070490888127421855230562476743437193669586130770874729998341806014505463783640697805066748097392661142651986383272569746929238370238236791611365888016395923937229663315669984045851361235492074956328026482075983768796861061848659835596192856014799478303800068654676296358731887087464680057625138685006784704860420472014154799635456877306821129665421051735463008716435484959281116736905095560434994978211883046937248916469787848011319675103042274669549285093478508496165293239267574405892054193071639761103531240880269213967720969569204405234720914506003137759701138818957384134064080297101555920650358158314638814808061444875629970967498629934896020014999531945611917565076555581463214259223983632596564284020547904568516382038627619926426399820079115184329439340506634492333929793888439430113573534410787213683675186757385099815814462452956461681614470787733950+n%2*188268005518720645667759037943290199729041576199713272258000341415142884489661357198413827336574563871710475891962386227254226548460457215784713632719207265722515532958111226770898448832976149694508611176171714812473191117942449486243536300166793001109750337816727112197364889073431978154829172861289718169113532600253115898758453827399772562770230003464760059000559575517913201138488702710174494988434408080060248054289370251263745124684792658352182826259739343112585674608618457651579839176917577105359817986057555885181280105441470666056823835660079537444179343557468143304791842405588449468759194267339411777317262475997047247874936511570970037411324036426865512945417642265038958781343979439726646347302832626941357993924180293499632367102400417024970463366842933311176081177500626536735139486456188568152499718609781595029945271755822729418702147805641561046500371225021414890598768720664317694974087527866510350196948714020904359944234084155381686049694559126527477298733016687942595626770233643747351407307621596986046980459655758729856670404142818843859210281075946102754581854676365225792628301159819898293949223127532065032026108487098977341039198791317194680237983244389072642823800530051714985602351769014420834910923563945731549656461682211742263452500430937532441080808786746799566843785373196638209540148360119199867838437711947537526070093086482313792740818047795954703870119555504292811253455020530957937699540875803660945840404921830972262588486787765278420728949598274917155854668063008139462714494853906539495543780533507991781350633386299997030671854397989793519872050638683868474243757990898795390055223603501757106626117644786159191030670806099279864843362386021540959176363197762329055526144596849982321651098254668285666591083867253252374306306512847236454590709088841350552210610685861103219815759548684268264164270572052102420991875915799674434602394372362711384408775338041123570773483588775964288272352363063084818552904239301974586747505288642716368742180470699534359078718311920500638515839349766386533021375201622204326841164210744009477740243367147426879348233166459771704835528012613633362210748777286340711696366755295670682654447409567525865460216116194229157054108960033556446081502372147862776652931222685155369111860836176979631269436382468481559169392856615459979599689145741831047615039007298460320003397886746197985203680048508828128354666360919960586327893891467221860220054134977506257669793994647578635978235220444255144351835530217987665584238403680995604538214694391013999058257550691861502797370211479920790397108505002637571629118064892007225396747960632407771502707217421954369163246932596308053144540610891441913623610305222246747464088896739298513218796580200605265122605338105564579876138902878716552171419408058480811534762139989163648474058791279434925548356025677200309718180290950130214509336449869774810751795948043738988701768574390671472494776788470985764780319650385523012251922679765290149888857208393004922759424736616535769338901469596625870241112985070588192999465319438923423131798139297805140252111547023102003338181698016651253765141895988759520075192717324927341200205914023406958703073098177779831415163295532216021446974286852182334970687378262386609452774118235061907906987519262027509050650729498176790704615089487487461666889239735767367434259640971308409975802988782900720060940702972339051996723516838317768179713374863322893473206918825912132276525225123999046471730880860759066006343556956703842041486381938083955699024965297138188180222288281791531022476637748726885879875552650789588729344865104679893125252459137253163723634936556574210191625561525643244553767888157405019079009648845900053568596416843330876607087218820681467908755438748960788860449866873325816827588589906998631459583072456115885452532446859593326880860870002593439370875262660050066596055227981838403252604188060750804793261107971617643851350903346868568550363780228952620975674722675397831564179597671316422621771281047205333696264391211981306723170366045190060807456763520436043801848217742747178242476232824934519476979740138422085204367902961433033493413548385940382883812962874003117089644785975824631484688663944651528324543595165040017984550966055986360343153899799769859388514498710963001632442066375519664523651762862899496100147262843217461590897583451755236383277449258804431719891572611460349970783973542272886749447137982867462547273552480877159746034766654650113825127209448947556640905116934600623969356264162539536635061744556374637351998660256568907237884606551421778494053651459245176133212647733338406060847388690560946859122514558261830816636811511096222144587892373702381884963433646735654628880000274175911461481526198984086261643580372157106518589096899308575849623421909113409586252481283952314518196465027159395827606929014439481368289049884590458665190133845748210249853612412782543757833818618043337650026848708398661019912276128488913830128909905203346732046346723779783533240991521256750588731069338751703947965311139606462614029929330499753226556074835789921703595710670238365226710944282873183557207380234166026418283025030463796722395703800011419915225261196057171067115278994513841754715762907518131756979283476505064435553180821820126829003463511890960353046422241286636626573529524701173705513630170500815003392538264953459393826911111515972765932318504111638211238865389866806408022815831926584923483423640084777638012177620268298323612765510934799584703242250877872463909087048117610841330581072250971396939495394618707498078492619942721916853041874472312695200690297618920098042612060301237772206718598123131309299232494188606035899354580920385942241820127253616277719745502011237887749581802411542240723241991830245400844874555074512283830490234340468250376862086869234034058879808968541015134089796525407677643926984536295506691627182840215921365459331700909678638689935588211487822206272374721590128440645395945186006719662188814485115870864006809591593224715493783281796534203052663834280633898982767729774833545833150024299118735956289888749933992645775953293294668802391766259946040725252838064971684913551470940567725464130733800877073578967694998819334959921185190756951405883507020509566539523303802494478381969697922698763401986457641685129972545293134705210262478610146271232825219397146410924858241094133520106642898308812111560515738514424881056072336352648583117467102939891838211169768861624788458088955005900899217729353059219290413783630957546470312899934568421221860232938611980822661609932072828296043172001678072954558816642938472789964709823287665398447916765442985311529516379561348532932303695494055449869844116409952753370982813741811244341771645999376222516207555994615675058574209793758362480453338627074405226935551190579721763549450242489340060198210540867581211194291004803309066725799820187960014805635629101497126629467481127895117669868694248150034873658969716157601278336023162387583741084430712431142019860008838942107502671771261341433242394282835202927490165498274155402725793986984136347262645681614912112361867629437859674081212948274966043226697282982828057275808060824558304851293855479015482300241498839973829827819186153027049624765526407161079522046007966456728797783341349609531094688831816555008274307643815921896130655247660623444801450272552150163209205765165527689135105193332061280431421522703034265271200594175242185109931325066362687322240964478232102443195536996147672002480120868672901494511026938701926664620231545448700742342559270998764048525872983084354561473916994233765402957807841809029638100055304733354145802382639897439619265375097902664216188235572863972658518521766278279726446964322073581335079427102675827258430844406613996545318636735795951772097283259038645065547665871050034289297936497336803295060875829929158260803334200890935268348259205279403296527666420130847685221407183317322194724423910997731332116891465343338631508201804705592104745418679748760678812719110608234942058077766480569116221173926125120600973671242278722907873403998856256288881968521311721321126419798115778606021805070631066426424295634141496756968195110237946272195026991911248006338170438866292749606908187846337173106045952388625163902213720356320825007848563259072037205951031665271513543492822988189550779265370705280068789076722286962640688916953559898479222160368200276534937676595823193016099017966337855405535061787679127347474937477701318579259332044536903402808119247223790982704335713708180376271761653131552016344249392387276349670419808984027531844025865738336890694427435267809041367218157756622747361605636912463723788934179580083210181670516609302725117440832837258697981951146529890409507306094044738013125712503334134358539561128964208933035168149875373065928637217994525728741193452047891823217723140904745005091313882388068316967326965490382295925707014766690283642476974767894230353614353279612421718381815894469899700853448857337842098202876500831250070906913793798517156974571403292479937745842017788301060341785202785268056236558026751904954514013568879507965683122126569361236409455588312107891210189551804095455827485117159016295269447879754784377973897865071331494381196718712859468731915591319147656837477009071421190513965232955023550076370180049997845341674111246513525487144668273538345431340300508622509871116704106029754872304762851277390376156444535853286975036178748554506566138510216536241305332115322349643199686417526912631136361)%((n%(9889608+n%2*59380)+63**31)*1922760350154212639070+1)

We submit this and get the flag. (There was a pow I wasn’t expecting which means I had to make the script interactive, but whatever.)

The flag is jail{i_hope_you_didnt_actually_implement_sha256...}.